2021. 8. 18. 14:41ㆍ프로그래밍/컴퓨터구조
※ http://kocw.net/home/cview.do?mty=p&kemId=1388791 영남대학교 최규상 교수님의 KOCW강의를 듣고 작성한 글입니다. ※
이번 강의에는 전공수업 디지털 공학에서 배운 내용이 많이 들어가 있었다.

음수를 타나내기 위한 2s-Complement Signed Integers
2의 보수 방식


Sign Extension
bit 수 증가할 때 어떻게 처리할 것인가
bit수는 증가했지만 나타내는 수는 같도록 해야한다.
- In MIPS Instruction set
- addi : 결국 immediate value값을 32 bit으로 바꾸어 레지스터에 더해주어야 한다.
- lb(load byte) , lh(load halfword) : 메모리로부터 1byte/halfwore(2byte) 받았을 때 32bit으로 바꾸어 레지스터(32bit)에 넣어줘야 한다.
- beq(branch equal), bne(branch not equal) : 값 비교시 그 값을 32bit으로 바꾸어 비교해주어야 함.
- Replicate the sign bit to the left c.f. unsigned values: extend with 0s
- Examples : 8-bit → 16-bit
- +2: 0000 0010 ⇒ 0000 0000 0000 0010
- -2: 1111 1110 ⇒ 1111 1111 1111 1110
Representing Instructions
- Instructions are encoded in binary ⇒ machine code라 불림
- MIPS Instructions
- All are Encoded as 32-bit instruction words
- operation code(opcode), register numbers등을 binary로 encoding하는 format이 많지 않음
- 그래서 MIPS Regularity 를 갖는다.
- Register Numbers
- $t0 - $t7 ⇒ register's 8 - 15
- $t8 - $t9 ⇒ register's 24 - 25
- $s0 - $s7 ⇒ register's 16 - 23
MIPS R-format Instructions
32bit는 그림과 같이 나누어져있다

- Instruction Fields
- op : operation code(opcode) - operation의 종류 나타냄
- rs : first source register number - 첫번째 source operand
- rt : target register, second source register number - 두번째 source operand
- rd : destination register number - rs와 rt 로 op의 operation을 해서 결과를 여기에 저장
- shamt : shift amount (00000 for now) - shift 연산과 관련
- funct : function code(extends opcode) - opcode를 확장한 것. 우리가 아는 arithmetic operations는 사실 function code로 결정된다. 어떤 operations들을 opcode로 다 표현할 수 없어 function code로 확장하여 나타낸다고 이해하면 된다.
R-format Examples
- add $t0, $s1, $s2

- add는 special opcode를 갖는다. special opcode: 0
- 보통 arithmetic operations는 special opcode를 갖는다.
⇒ 즉, 명령어로 000000 10001 10010 01000 00000 100000 이 코드를 만나면 add $t0, $s1, $s2 연산을 실행한다 . machine code
Hexadecimal (16진수)
Base 16
- bit strings의 compact representation
- hex digit 당 4 bits
- (예) eca8 6420 → 1110 1100 1010 1000 0110 0100 0010 0000

MIPS I-format instructions

- Immediate arithmetic and load/store instructions
- rt : destination or source register number (예) load명령어라면 destination이고 store명령어라면 source가 될 것이다.
- Constant(immediate) : $-2^{15}$ ~ $+2^{15}-1$ (16bit이기때문에)
- Address : rs의 base address에 더해지는 offset
Design Principle
- Good design demands good compromises
- different formats complicate decoding, but allow 32-bit instruction uniformly
- Keep formats as similar as possible
⇒ arithmetic명령어와 load/store명령어는 종류나 하는 일이 다른 아주 별개의 명령어이지만, 두 명령어 타입이 같은 format을 사용한다. 다른 format이라면 decoding이 아주 복잡해질 것이다.
⇒ format의 수를 줄이는 것이 중요하다 (simplicity → faster 위해서)
Stored Program Computers

- instructions는 data처럼 binary로 표현된다
- instructions와 data는 memory에 stored
- 어떤 프로그램들은 프로그램에 동작한다 (예) compilers, linkers, ...
- binary compatibility는 compiled programs가 다른 컴퓨터에서도 동작할 수 있게 해준다. (예) Standardized ISAs
Logical Operations
- bitwise manipulation위한 Instructions

Shift Operations

- shamt: 몇bit만큼 움직일 것이냐
- shift left logical
- shift left and fill with 0 bits
- sll by i bits multiplies by $2^i$
- shift right logical
- shift right and fill with 0 bits
- srl by i bits divides by $2^i$ (unsigned only)
AND Operations
and $t0, $t1, $t2→ t1과 t2를 and 연산하여 t0에 저장한다

- 특정 값을 masking하는데 유용하다.
- 특정 bit값을 뽑아내거나 다른 값들은 다 0으로 만들 때
OR Operations
or $t0, $t1, $t2 → t1과 t2를 or연산하여 t0에 저장한다.
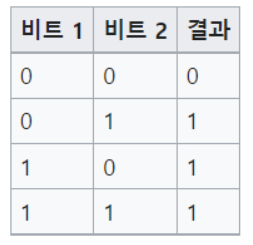
어떤 bit는 1로 세팅하고 나머지는 바뀌지않도록 할 때 유용
NOT Operations
MIPS에선 NOT operation을 지원하지 않지만 NOR operation을 이용하여 NOT을 구현한다.
nor $t0, $t1, $t2 → t1과 t2의 nor연산 결과를 t0에 저장
not연산을 위해서는
- nor $t0, $t1, $zero를 해준다. zero와 t1의 or연산 결과는 항상 t1 → 결국 not t1의 결과가 t0에 저장된다
- ※ $zero는 Resistor 0로, 항상 0을 읽는다

- complement, 즉 bit를 invert할 때 유용
- 0을 1로, 1을 0으로 변경
- MIPS 는 NOR 3-operand instruction을 갖는다.
- a NOR b == NOT(a OR b)
Instructions for Making Decisions
Conditional Operations
- Branch명령어 : Branch to labeled instruction if a condition is True
- Otherwise, continue sequentially
- beq rs, rt, L1
- rs==rt이면 branch to instruction labeled L1
- bne rs, rt, L1
- rs!=rt이면 jump to instruction labeled L1
- j L1
- unconditional jump to instruction labeled L1 (무조건)
Compiling If Statements
- C code의 경우
- if (i==j) f=g+h; else f = g-h;
- f, g ...in $s0, $s1, ...
↓ 컴파일해 MIPS assembly언어로
- Compiled MIPS code의 경우
- bne $s3, $s4, Else add $s0, $s1, $s2 j ExitExit: ...
- Else: sub $s0, $s1, $s2
Compiling Loop Statements
- C code의 경우
- while (save[i] == k) i += 1;
- i in $s3, k in $s5, address of save in $s6
- save는 integer array
- while (save[i] == k) i += 1;
- Compiled MIPS code:
- Loop: sll $t1, $s3, 2 → s3 x 4⇒t1 add $t1, $t1, $s6 → t1 + s6 ⇒ t1 lw $t1, 0($t1) → t1 + 0(offset) ⇒ t1 = save 의 base주소에서 32bit 읽어 t1에 넣어주는 것 bne $t0, $s5, Exit → t0와 k값 비교 addi $s3, $s3, 1 → i값 1만큼 증가 j Loop → Loop으로 다시 돌아가! Exit: ...
Basic Blocks
Basic block은 이러한 명령어들의 시퀀스이다
- 맨 끝을 제외하고 embedded branch가 없다.
- 시작을 제외하고 branch target이 없다 .
컴파일러는 최적화를 위해 basic block을 찾는다.
advanced processor는 basic block의 실행을 가속화 시킬 수 있다.
More Conditional Operations
- set result 1 if a condition is true. otherwise, set to 0
- slt rd, rs, rt
- if (rs<rt) rd = 1; else rd=0;
- slti rt, rs, constant
- if (rs<constant) rt = 1; else rt=0;
- slt rd, rs, rt
- beq, bne 함께 쓰기
- slt $t0, $s1, $s2 # if ($s1<$s2) bne $t0, $zero, L # branch to L
Branch Instruction Design
blt, bge 등을 왜 쓰지 않을까?
- <, ≤ 등에서 하드웨어는 =, ≠ 보다 느리다 = 구현이 어렵다
- branch를 합치는 것은 명령어당 더 많은 일을 요구하고
- clock이 느려진다
- 모든 명령어들은 clock에 동기화되어 있기 때문에
- 모든 명령어들이 penalized! (느려진다)
- beq와 bne는 common case이다.
- 복잡한 명령어를 지원하는 것 보다는 common case, 간단한 명령어를 여러번 사용하는 것이 성능이 더 좋을 수 있다.
- 이것은 good design compromise이다.
Signed, Unsigned
Signed comparison : slt, slti
Unsigned Comparison : sltu, sltui
Example
- $s0 = 1111 1111 1111 1111 1111 1111 1111 1111
- $s1 = 0000 0000 0000 0000 0000 0000 0000 0000
- slt $t0, $s0, $s1 # signed
- -1 < +1 ⇒ $t0 = 1
- sltu $t0, $s0, $s1 # unsigned
- +4,294,967,295 > +1 ⇒ $t0 = 0
'프로그래밍 > 컴퓨터구조' 카테고리의 다른 글
| 컴퓨터구조 4주차 -1 (0) | 2021.08.20 |
|---|---|
| 컴퓨터구조 3주차 -1 (0) | 2021.08.11 |
| 컴퓨터 구조 2주차 (0) | 2021.08.06 |
| 컴퓨터구조 1, 2강 (0) | 2021.07.30 |